Electrical Resistance
The electrical resistance of any substance is a measure of its opposition to electric current passing through it.
When a voltage is applied across a substance, it will have an electric current through it. The applied voltage through the substance is directly proportional to the current passing through it. Therefore resistance is defined as the proportion of the applied voltage to the current passing through the substance.
The conductor has free electrons. When the voltage is applied in the conductor, then free electrons start moving in a particular direction. During the movement, these electrons strike with the conductor's atoms and molecules. Atoms or molecules create a barrier in the flow of electrons. This barrier is called resistance.
Electrical resistance is given to the circuit by the resistor. Resistance indicates the relationship between the applied voltage and the flow of charges. Resistance is inversely proportional to the flow of current.


Some materials are mostly metal that provides very low resistance to current passing through them. These materials are referred to as the electrical conductor.
There is another type of materials called semiconductor which offers moderate value of resistance to current passing through them.
The materials which offer extreme resistance to the current passing through them is known as the insulator.
Resistance calculation
There should be resistance in every material. The resistance to the material in which high conductivity is low. however, the material whose resistance is low has more conductivity. The ohmmeter measures electrical resistance. The resistance of the wire depends on the length and cross-section area of the wire.
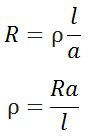
Resistance in series
The total equivalent resistance of the resistor in the series is the sum of the resistance of resistors
Rtotal = R1+R2+R3+.......

Resistance in parallel
The total equivalent resistance of the resistor in the parallel is given by -
1/Rtotal = 1/R1 + 1/R2 + 1/R3

Temperature coefficient of Resistance
Interatomic vibrations increase in metallic substances with increasing temperatures, and hence it provides greater resistance to the movement of electrons, causing the current. Therefore, resistance to metal materials increases with increasing temperature. The temperature coefficient of resistance for these materials is positive.
Increasing temperature increases the number of high electrons in semiconductors because covalent bonds at high temperatures are broken down to contribute to free electrons in the substance. This reduces resistance to substance. Therefore, there is a negative temperature coefficient in semiconductors.



